
Multiplying and dividing by constants performs stretch and compression effects.

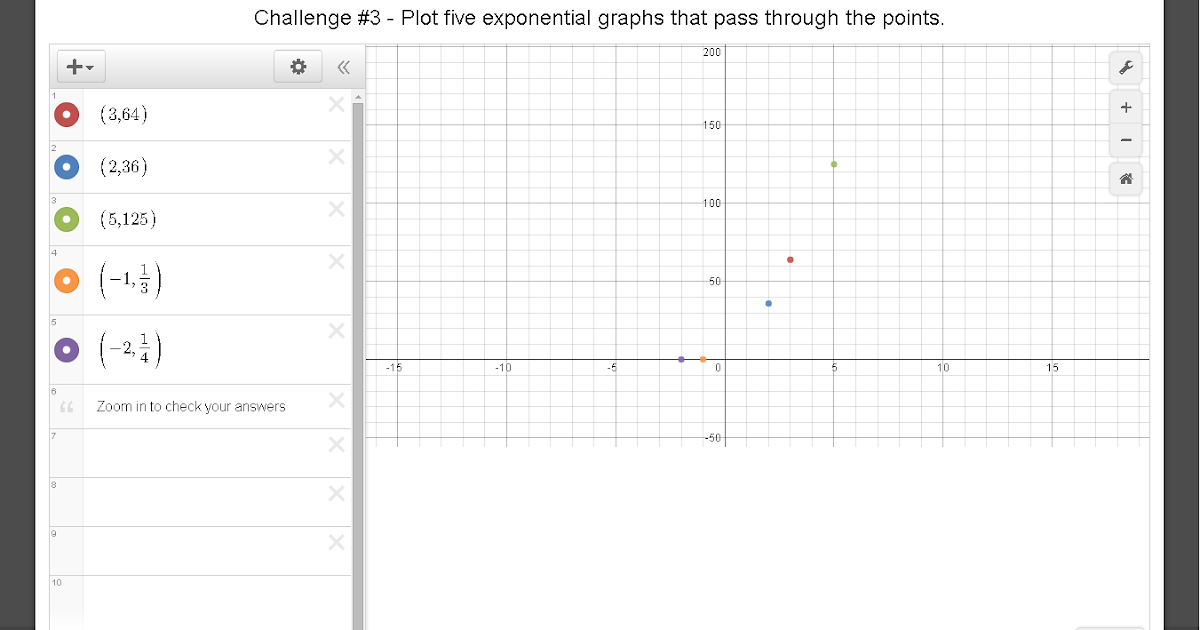
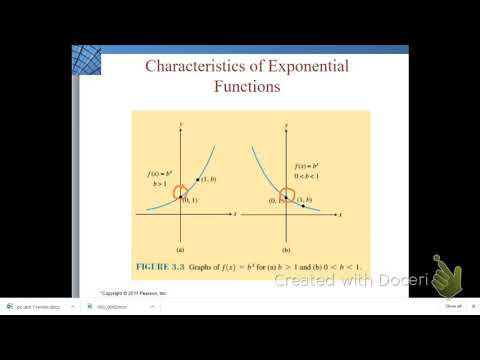
Adding and subtracting constants perform translations on functions.Logarithmic graphs grow very slowly as tends to infinity.Exponential graphs grow very quickly as tends to infinity.Connect the points with an exponential curve, following the horizontal asymptote. EXAMPLE 3 Finding key features on an exponential graph Making. Plug in a few easy-to-calculate points, like x 1, 0, 1 x-1, 0, 1 x 1, 0, 1 in order to get a couple of points that we can plot. In Example 2, note that whether the exponential function is increasing or decreasing. Knowledge of exponent and logarithm graphs, as well as functional transformations are encouraged to ensure success on this exercise. The real-number value is the horizontal asymptote of the exponential function. Match the exponential function with it's graph The student is asked to match each function with the correct graph. Match the exponential function with its graph: This problem provides a set of graphs and rules for some logarithmic functions.The student is asked to drag the correct exponential function that matches the formula of the function. Graph the exponential function: This problem provides an interactive graph with coordinates.There are two types of problems in this exercise: This exercise practices graphing exponential functions and find the appropriate graph given the function. The Graphs of exponential functions exercise appears under the Algebra II Math Mission and Mathematics III Math Mission. This relationship enables the determination of all values, as long as at least one is known.Algebra II Math Mission, Mathematics III Math Mission Using the above equations, it is also possible for a relationship to be derived between t 1/2, τ, and λ. This SKILL BUILDER supports students ability to apply these growth models to real-world scenarios. Derivation of the Relationship Between Half-Life Constants Students have developed an understanding of key concepts in population ecology and learned to model population growth rates as exponential or logistic. This means that the fossil is 11,460 years old. If an archaeologist found a fossil sample that contained 25% carbon-14 in comparison to a living sample, the time of the fossil sample's death could be determined by rearranging equation 1, since N t, N 0, and t 1/2 are known. N t is the remaining quantity after time, t The carbon-14 undergoes radioactive decay once the plant or animal dies, and measuring the amount of carbon-14 in a sample conveys information about when the plant or animal died.īelow are shown three equivalent formulas describing exponential decay: Base: Exponent: If the calculator did not compute something or you. It is incorporated into plants through photosynthesis, and then into animals when they consume plants. This calculator will calculate the exponential function with the given base and exponent. The process of carbon-14 dating was developed by William Libby, and is based on the fact that carbon-14 is constantly being made in the atmosphere. The half-life of carbon-14 is approximately 5,730 years, and it can be reliably used to measure dates up to around 50,000 years ago. Interpret, compare, and translate between multiple representations of an algebraic function. Compose functions to create a new function.
Predict outputs of a function using given inputs. One of the most well-known applications of half-life is carbon-14 dating. Define a function as a rule relating each input to exactly one output and predictably acting on inputs. The term is most commonly used in relation to atoms undergoing radioactive decay, but can be used to describe other types of decay, whether exponential or not. Students will test their ideas by launching the marbles and will have a chance to revise before trying the next challenge. Half-life is defined as the amount of time it takes a given quantity to decrease to half of its initial value. In this delightful and challenging activity, students will transform exponential functions so that the marbles go through the stars.


 0 kommentar(er)
0 kommentar(er)
